Why Math Feels Impossible (And Why That’s Normal)

If you’ve ever found yourself staring at a math problem and felt a wave of panic wash over you, you are definitely not alone. It’s a common feeling, but it doesn’t mean you’re “bad at math.” The truth is, the whole idea of a “math person” is pretty much a myth. This belief—that some people are just born with a math brain and others aren’t—holds so many students back.

The real reason most people struggle with maths isn’t a lack of natural talent; it’s because of how the subject is built. Unlike history, where you can study the Tudors without knowing much about ancient Rome, math is like building a tower. Each new concept is a block placed on top of the ones that came before. If a few blocks in your foundation are wobbly—say, you never really got the hang of fractions or negative numbers—the whole structure gets shaky when you try to add algebra or calculus on top. These small gaps in understanding add up over time, making you feel completely lost when you might only need to go back and strengthen an earlier skill.

The Problem Isn’t You, It’s Often the Approach

Sometimes, the way maths is taught can make things harder. A heavy focus on memorising formulas without understanding why they work can turn math into a set of confusing rules instead of a logical puzzle. This is where many students tune out. This is a widespread issue, and it’s reflected in national trends.

For instance, data from the OECD’s PISA assessment shows a worrying decline in maths performance across Australia over the past decade. A huge 40% of 15-year-old students are now failing to meet minimum national standards. They particularly struggle to connect mathematical ideas to real-world situations. You can explore a detailed vision for how to turn this trend around and improve mathematical education for Australian students.

The key to learning how to get better at math is to reframe these struggles. Getting confused is a normal, even essential, part of learning. Successful students see a tough problem not as proof of failure, but as a signpost pointing to a weak spot in their knowledge. They get curious about their confusion. Shifting your mindset like this is the first real step towards building confidence.

Understanding Your Learning Roadblocks

Recognising why you’re stuck is a superpower. When you hit a wall, ask yourself a few questions:

• Is it a knowledge gap? Is there a term or an older concept being used that I don’t fully understand?
• Is it the language? Am I getting lost in how the problem is worded?
• Is it a strategy issue? Do I get the concepts but just have no idea where to start solving the problem?

Below is a look at the homepage for the PISA assessment, which gathers data on student performance from all over the world.

This screenshot shows the global scale of educational assessment, giving us insights that help us understand these challenges are not just personal, but system-wide. By figuring out the source of your difficulty, you can take targeted action instead of feeling overwhelmed by the entire subject.

Building Unshakeable Math Foundations

Have you ever tried to learn calculus when you’re still a bit fuzzy on fractions? It’s like trying to build a house on a swampy patch of land—it’s just not going to hold up. The real secret to learning how to get better at math is making sure your core skills are absolutely solid. Before you can tackle the tough stuff, you need to be honest with yourself about where the gaps are hiding. This isn’t about feeling bad about what you don’t know; it’s a smart strategy to build a foundation that can support anything you learn later.

So, how do you find these weak spots without re-doing every math worksheet from Year 7? You need to become a bit of a detective. The next time you get stuck on a problem, don’t just blame the new, complex topic. Instead, break the problem down into its smallest parts. Are you fumbling with the algebra? Is it the arithmetic with negative numbers that’s tripping you up? Pinpointing that exact moment of confusion is your biggest clue.

Finding and Fixing the Cracks

Let’s be honest: practising multiplication tables or the rules for integers can feel like a chore, especially when you want to solve more interesting problems. But mastering these fundamentals is non-negotiable. A common trap students fall into is studying just enough to pass a test, only for that same weak spot to cause trouble down the line. The aim isn’t just to be familiar with the basics; it’s to achieve automaticity. You want to be able to do these simple calculations without even thinking, freeing up your brainpower for the trickier logic of the main problem.

Here’s a practical approach to assessing and strengthening your foundational skills:

• Keep a “Stuck List”: Start a running list in a notebook of every specific concept that makes you pause. It could be anything from “dividing by decimals” to “rearranging equations to solve for x”.
• Do Targeted Drills: Spend short, focused bursts of time—even 15 minutes a day—on just one thing from your list. Keep at it until it feels easy.
• Explain It Out Loud: A great test of mastery is trying to teach a concept to someone else, or even just explaining it to your bedroom wall. If you can’t explain it simply and clearly, you haven’t quite got it yet.

To help you get started on this, I’ve created a simple checklist. Go through it honestly and rate your confidence in each area. This will give you a clear map of what to work on first.

Mathematical Foundation Skills Assessment
A comprehensive checklist to identify which fundamental skills need strengthening across different mathematical areas

Skill Area	Key Concepts	Self-Assessment Rating (1-5, 1=Weak, 5=Strong)	Priority Level (High, Medium, Low)
Arithmetic	Addition, Subtraction, Multiplication, Division
	Operations with fractions and decimals
	Order of Operations (BODMAS/PEMDAS)
	Percentages and Ratios
Pre-Algebra	Integers and negative numbers
	Variables and expressions
	Solving single-variable linear equations
	Exponents and square roots
Algebra 1	Solving multi-step equations
	Graphing linear equations (slope, intercepts)
	Systems of equations
	Factoring polynomials
Geometry	Area, Perimeter, and Volume formulas
	Pythagorean theorem
	Properties of angles and shapes

Once you’ve filled this out, you’ll have a much better idea of your personal “high priority” items. Start with those, and you’ll see a massive improvement in your confidence and ability.

This foundational work takes time, and your progress won’t always be a straight line. Some days will feel like a massive breakthrough, while others might feel like you’re stuck in the mud. That’s completely normal. The key to staying motivated is to celebrate the small victories, like when you finally nail operations with negative numbers. This consistent effort is an investment that pays off big time, making all your future learning so much smoother.

Study Methods That Actually Make Math Stick

Once your foundations are solid, it’s time to rethink how you study. Just reading a textbook or mindlessly doing dozens of the same type of practice problem is one of the least effective ways to learn. To genuinely improve at math, you need active, strategic study methods that push your brain to connect with the material on a much deeper level. Let’s move past passive learning and into techniques that build real, lasting understanding.

The Feynman Technique: Explain It to Understand It

One of the best ways to test if you truly understand something is to try explaining it simply. That’s the whole idea behind the Feynman Technique. After you learn a new concept, take a blank piece of paper and write down everything you know about it as if you were teaching a ten-year-old. Use your own words and simple analogies.

Where do you get stuck? Where do you find yourself using complicated jargon because you can’t simplify it? Those are your exact knowledge gaps. Go back to your notes or textbook, figure out that specific point, and then try explaining it again. This process turns abstract rules into concrete knowledge you can actually use.

Spaced Repetition and Interleaving: Your Brain’s Best Friends

Cramming for an exam might get you a pass, but that information will probably be gone a week later. The brain learns far better when it revisits information over increasing periods. This method is called spaced repetition. Instead of a single four-hour study session, try four separate one-hour sessions spread throughout the week. This approach works with your brain’s natural rhythm to interrupt the forgetting process.

Here’s a look at the “forgetting curve,” which shows how spaced repetition helps you hold onto information for longer.

As the graph shows, each time you review the material, you forget it more slowly, which is the key to long-term retention.

Combine this with interleaving, which is just a fancy way of saying you should mix up different types of problems in one study session. Instead of doing 20 problems on quadratic equations, do five on quadratics, five on geometry, and five on probability. It feels more difficult at first, but it trains your brain to recognise which strategy to use for a given problem—a vital skill for exams.

This builds flexible thinking, which is crucial for applying math in the real world. For example, recent findings show Australian students perform best in areas like ‘uncertainty and data’, which involves using different statistical and probability concepts to make sense of information. You can discover more about these findings from the PISA report analysis. Building this kind of adaptable skill through interleaving is exactly how you prepare for complex, real-world challenges.

Cracking Problems Like a Mathematical Detective

Problem-solving is where maths gets truly interesting, but it’s also where many of us hit a wall. When you’re staring at a problem that looks completely unfamiliar, it’s easy to freeze up. The secret isn’t about having all the answers memorised; it’s about having a process to find them. Think of yourself as a detective arriving at a crime scene. You don’t know who did it, but you know how to look for clues, gather evidence, and piece together the story. This methodical approach is a core part of learning how to get better at math.

The first move is always to read and understand the problem deeply. Don’t just skim it. What information are you given? What, exactly, is the question asking you to find? Sometimes, just rephrasing the problem in your own words or drawing a simple diagram can make everything click. It’s about slowing down to go faster.

Developing Your Mathematical Intuition

Once you understand the goal, you can start looking for patterns. Does this problem resemble anything you’ve solved before? Even a small similarity can be a clue. This is where you start building your mathematical intuition—that gut feeling for which approach might work. You can’t force intuition, but you can cultivate it by exposing yourself to a wide variety of problems and paying attention to the connections between them. This strategic thinking is far more valuable than simply following a procedure you’ve been taught.

To help you build this intuition, it’s useful to have a toolkit of strategies you can draw upon. Different problems call for different approaches, and knowing which one to pick is a skill in itself.

Here’s a table to help you decide which strategy to use and when.

Problem-Solving Strategy Toolkit

A practical guide showing when and how to apply different problem-solving approaches based on problem type and complexity

Strategy	Best Used For	Key Steps	Example Application
Drawing a Diagram	Problems involving geometry, physical space, or relationships between objects.	1. Sketch the scene described. 2. Label all known quantities. 3. Identify what you need to find on the diagram.	Calculating the area of a garden with a path around it. A diagram makes it easy to see the inner and outer rectangles.
Working Backwards	When the final outcome is known, but the initial state is not.	1. Start with the end result. 2. Reverse each operation step-by-step. 3. Continue until you reach the starting point.	You have $50 left after shopping. You spent $20 on a t-shirt and half of your remaining money on lunch. How much did you start with?
Finding a Pattern	Sequences, series, or problems with repeating elements.	1. Solve for the first few simple cases. 2. Write down the results in order. 3. Look for a relationship or rule between consecutive terms.	Finding the 100th number in the sequence 2, 5, 8, 11… You notice the pattern is “add 3,” then generalise it.
Making a Table	Organising data or tracking multiple variables.	1. Set up columns for each variable. 2. Fill in the table with information from the problem. 3. Use the organised data to find relationships or solve the problem.	A problem about coin combinations (e.g., how many ways to make $1 with 10c and 20c coins). A table can track the number of each coin.

This toolkit isn’t a magic formula, but it gives you a starting point when you feel stuck. The more you practice applying these strategies, the more intuitive it will become to select the right one for the job.

Different problem types also respond better to certain learning styles. Modern resources can help sharpen these skills. This infographic compares the average score improvements from three popular digital learning tools.

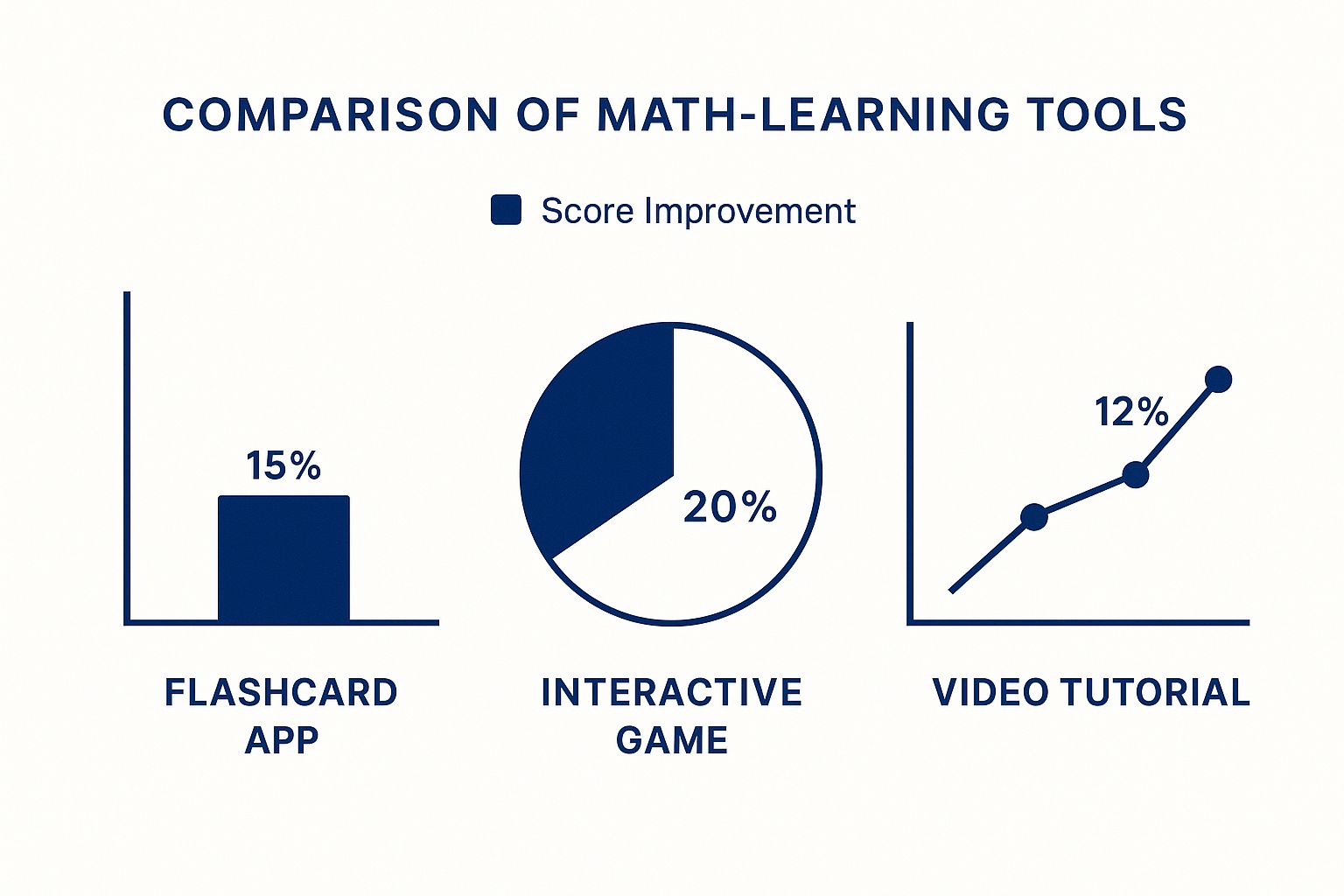
The data suggests that interactive games, which often focus on strategic problem-solving, can lead to a 20% improvement in scores. This highlights the value of engaging, active practice over passive learning.

Staying Calm and Checking Your Work

The final, crucial part of the detective process is verification. After you’ve reached a solution, plug it back into the original problem. Does it make sense? A common mistake is stopping as soon as you have an answer on the page. Expert problem-solvers always double-check their work, not because they lack confidence, but because they are thorough. They question their own assumptions and look for potential errors.

Building this persistence takes practice. It’s about developing the grit to stick with a problem even when it feels impossible. By adopting this detective mindset—read, analyse, strategise, and verify—you’ll not only solve more problems correctly but also build the deep, flexible thinking skills that define what it means to be good at maths.

Getting Help Without Feeling Defeated

One of the hardest parts of learning **how to get better at math** is knowing when to keep pushing through a tough problem and when it’s time to ask for help. It’s a delicate balance between productive struggle and simply hitting a brick wall. The truth is, seeking help effectively is a skill in itself—one that even the most accomplished mathematicians rely on.

So, how do you know when you’re really stuck? A good rule of thumb is to assess your effort. Have you tried a few different approaches? Did you go back and review the core concepts related to the problem? If you’ve spent a decent amount of time on a single problem with nothing to show for it but a blank page and a growing headache, that’s your cue. It’s not a sign of failure; it’s a signal that a fresh perspective is needed.

Making Your Cry for Help Productive

Just saying, “I don’t get it,” doesn’t help you or the person you’re asking. To get the most out of a session with your teacher or a study group, you need to be more specific with your questions.

• Pinpoint your confusion: Before you ask, figure out the exact point where you got lost. Instead of a general plea, try something like, “I was fine setting up the equation, but I got stuck when I had to simplify the negative exponents.”
• Show what you’ve tried: Always bring your work, even the messy, incorrect parts. This gives your teacher or study partners a window into your thought process. They can then correct a specific misunderstanding instead of re-teaching the entire topic from the beginning.
• Form a study group: Working with your peers is a powerful tool. Explaining concepts to others helps solidify your own understanding, and you’ll quickly find out you’re not the only one struggling with certain topics. This shared experience can reduce the sense of isolation that often comes with math challenges.

Getting support is particularly important, especially considering some of the challenges in the Australian education system. For instance, 2023 data revealed that only 13% of Australian Year 4 students were performing at an advanced level in a major international maths test, a figure lagging behind many other countries. This points to broader issues that can make it tough for students to keep up without extra help. You can read more about the plan to reboot maths in Australian schools to understand the context better.

Ultimately, asking for help is a strategic move, not a weakness. Whether you turn to a teacher, a friend, or an external resource, the right support can transform a frustrating roadblock into a valuable learning opportunity. If you’re thinking about more formal support, it might be useful to explore the reasons to opt for tuitions and see if it’s the right path for you.

Finding Math Everywhere (And Loving It)

One of the biggest mental shifts you can make on your journey to get better at math is to stop seeing it as something that only exists in a classroom. Mathematics isn’t just a string of abstract problems in a textbook; it’s the language that describes the world around us. When you start to see it in action, it changes from a chore you have to get through into a powerful and practical toolkit for everyday life. This change in perspective is a huge step in learning how to get better at math.

The famous mathematician Paul Halmos once said, “The only way to learn mathematics is to do mathematics.” He wasn’t just talking about worksheets. He meant applying mathematical thinking to your hobbies, your finances, and even what you do in the kitchen. For instance, when you’re cooking from a recipe and need to double the ingredients or cut them in half, you’re working with ratios and proportions. When you’re putting together a budget to save for a new phone, you’re using percentages and basic algebra to track your progress and plan your spending.

Turning Daily Life into a Math Lab

Once you start looking, you’ll find mathematical concepts hiding in plain sight. This image shows just how interconnected all the different fields of mathematics are.

This web of connections isn’t just a theory; you can see it playing out in your own life.

The goal is to actively look for these moments and use them as informal practice. Don’t just guess your grocery bill; do a quick mental calculation as you shop. Don’t just admire a piece of architecture; notice the geometric shapes, symmetry, and patterns the architect used.

Here are a few ways to start spotting math in your environment:

• At a Café: Try to estimate the total cost of your order before you get to the counter. When you pay, calculate the change you should receive.
• While Driving: Use the distance to your destination and your average speed to estimate your arrival time. Think about the geometry involved in parking in a tight spot.
• Planning Your Weekend: Juggling appointments, social events, and chores is a real-world logic problem that relies on scheduling and time management.

From Dread to Appreciation

Using real-world problems to reinforce what you’re learning makes the concepts stick because they suddenly have context and meaning. Instead of just solving for x on a page, you’re solving for how much you need to save each week to buy that new video game. This practical application builds a genuine appreciation for mathematics as an elegant problem-solving tool.

For students who need a bit more guidance making these connections, exploring the benefits of private tutoring can show how personalised attention helps bridge the gap between classroom theory and real-world application. The more you see math as a useful part of your life, the less mysterious and intimidating it becomes.

Your Personal Math Improvement Action Plan

All the strategies and mindset shifts we’ve talked about are powerful, but they work best when organised into a routine you can actually stick with. Let’s build a practical roadmap you can start using today. This isn’t about finding more hours in the day; it’s about making the hours you have really count. Real, lasting improvement in maths comes from consistency, not just short bursts of intensity.

Setting Up a Sustainable Routine

To get better at maths, you need a plan that fits your life. A realistic structure helps prevent burnout and keeps you moving forward, even when your motivation takes a dip. A great plan should include daily practice, weekly reviews, and monthly check-ins.

• Daily Practice (20-30 minutes): Think of this as your core workout. Spend this time actively solving problems, not just passively reading. Use the interleaving technique we talked about—mix up new concepts with older ones. This is brilliant for strengthening your long-term memory.
• Weekly Review (45-60 minutes): Once a week, set aside time to go through your “stuck list” and notes from the past few days. Try using the Feynman Technique to explain the toughest concept of the week to yourself out loud. This session is for cementing what you’ve learned, not for cramming new material.
• Monthly Check-in (30 minutes): At the end of each month, take a moment to look at your progress. Do you feel more confident with topics that were tricky before? Try re-taking a small quiz or re-doing a few tough problems from the start of the month. This helps you see how far you’ve come and what to focus on next.

Overcoming Plateaus and Setbacks

Progress is never a perfect straight line. You will hit plateaus where it feels like you’re stuck in the mud and not getting any better. This is a completely normal part of learning. When this happens, just pushing harder with the same old methods probably won’t work. Instead, it’s a sign that you need to change your approach.

If you’re stuck, try working backwards from a solved example in your textbook. Seeing how a correct solution is put together can often shine a light on a missing step in your own thinking. Another fantastic strategy is to switch topics completely for a day or two. Giving your brain a break from one type of problem can often lead to a breakthrough when you come back to it with fresh eyes.

Remember that consistent, focused effort over time is the most reliable path to success. Don’t get disheartened by a tough day or a difficult week. Every problem you wrestle with, even the ones you don’t solve right away, is building your mathematical muscle. This journey is a marathon, not a sprint, and your persistence is your greatest asset. By putting a solid plan in place and treating setbacks as chances to learn, you create a powerful system for growth.

Feeling like you could use some expert guidance to help create and stick to your plan? The team at NRICH Learning specialises in providing the personalised support that turns mathematical challenges into achievements. We help students build foundational skills and develop the confidence to succeed. Explore our K-12 tutoring programmes to see how we can support your journey.